2的平方根-2的平方根,2,平方,根

2的算数平方根是多少？

2的算数平方根是√2≈1.414。 这里需要注意算数平方根和平方根的区别：正数有两个平方根,他们互为相反数,负数没有平方根,0的平方根是0非负数的算术平方根只有一个。这里需要计算时的算术平方根√2≈1.414。 扩展资料： 算数平方根和平方根的区别： 1、定义不同，平方根的定义，若x的平方等于a，则a为x的平方根。 2、算术平方根的定义，一个非负数的正的平方根叫做它的算术平方根。 3、个数不同，正数的平方根有两个且互为相反数，正数的算术平方根只有一个。 4、表示方法不同，平方根：a的平方根为正负根号a；算术平方根：a的算术平方根为根号a。

2的平方根是多少？

正数a的平方根有两个，为±√a，
所以，2的平方根是±√2。

2的平方根是多少/

正负根号2 约等于正负1.4142 算术平方根是根号2

九的算术平方根是多少

列式计算为
√9=3
所以9的算术平方根为3.

二的平方根是多少啊！

2的平方根是正负根号2约等于正负1.414

根号2开方的计算方法

算法1：
假设被开放数为a，如果用sqrt（a）表示根号a那么(（sqrt(x)-sqrt(a/x))^2=0的根就是sqrt（a）
变形得
sqrt(a)=（x+a/x）/2
所以你只需设置一个约等于（x+a/x）/2的初始值，代入上面公式，可以得到一个更加近似的值，再将它代入，就得到一个更加精确的值……依此方法，最后得到一个足够精度的（x+a/x）/2的值。
如：计算sqrt(5)
设初值为2
1)sqrt(5)=(2+5/2)/2=2.25
2)sqrt(5)=(2.25+5/2.25)/2=2.236111
3)sqrt(5)=(2.236111+5/2.236111)/2=2.236068
这三步所得的结果和sqrt(5)相差已经小于0.001
或者可以用二分法：
设f(x)=x^2-a
那么sqrt(a)就是f(x)=0的根。
你可以先找两个正值m,n使f(m)0
根据函数的单调性，sqrt(a)就在区间（m，n）间。
然后计算（m＋n）/2，计算f（（m＋n）/2），如果它大于零，那么sqrt(a)就在区间（m，（m＋n）/2）之间。
小于零，就在（（m＋n）/2，n）之间，如果等于零，那么（m＋n）/2当然就是sqrt(a)。这样重复几次，你可以把sqrt(a)存在的范围一步步缩小，在最后足够精确的区间内随便取一个值，它就约等于sqrt(a)。

开平方公式

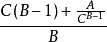
关于任意数开任意次方的公式：设被开方数为A，开次方数为B。C为变量 首次C取值为1，带入A,B常量计算结果，并用计算结果值替换公式中的变量 C。再次计算结果，再次替换，当C=公式计算结果值，此时C即为根。循环步骤受开方数字长度影响，此法也可笔算进行。采用的是牛顿迭代法。 且 A、B 可为小数，分数，负数，此法为逐次逼近法。可简单的实现编程。但是注意：不能计算负数开偶数次方。 扩展资料 相关应用： A=5：5介于2的平方至3的平方;之间。我们取初始值2.1，2.2，2.3，2.4，2.5，2.6，2.7，2.8，2.9都可以，我们最好取 中间值2.5。 第一步：2.5+（5/2.5-2.5)1/2=2.2； 即5/2.5=2，2-2.5=-0.5，-0.5×1/2=-0.25，2.5+(-0.25)=2.25，取2位数2.2。 第二步：2.2+(5/2.2-2.2)1/2=2.23； 即5/2.2=2.272，2.272-2.2=0.072，0.072×1/2=0.036，2.2+0.036=2.23。取3数。 第三步：2.23+(5/2.23-2.23)1/2=2.236。 即5/2.23=2.242,2.242-2.23=0.012,0.012×1/2=0.006,2.23+0.006=2.236. 每一步多取一位数。这个方法又叫反馈开方，即使你输入一个错误的数值，也没有关系，输出值会自动调节，接近准确值。

在excel中开平方的公式是什么，2次方的公式是什么

同一个函数：POWER 1、平方的计算 如下图，在函数表达式栏输入“=POWER(B4,2)后回车，则计算B4栏数据的平方 2、算术平方根的计算与平方的计算方法类似，只需将上述表达式中的“2”改为“0.5”即可。

怎么用计算方法开平方

原理:设被开方数为X,开n次方,设前一步的根的结果为a,现在要试根的下一位,设为b,
则有:(10*a+b)^n-(10*a)^n<=c(前一步的差与本段合成);且b取最大值
用纯文字描述比较困难,下面用实例说明:
我们求
2301781.9823406
的5次方根:
第1步:将被开方的数以小数点为中心,向两边每隔n位分段(下面用'表示);不足部分在两端用0补齐;
23'01781.98234'06000'00000'00000'..........
从高位段向低位段逐段做如下工作:
初值a=0,差c=23(最高段)
第2步:找b,条件:(10*a+b)^n-(10*a)^n<=c,即b^5<=23,且为最大值;显然b=1
差c=23-b^5=22,与下一段合成,
c=c*10^n+下一段=22*10^5+01781=2201781
第3步:a=1(计算机语言赋值语句写作a=10*a+b),找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:(10+b)^5-10^5<=2201781,
b取最大值8,差c=412213,与下一段合成,
c=c*10^5+下一段=412213*10^5+98234=41221398234
第4步:a=18,找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:(180+b)^5-180^5<=41221398234,
b取最大值7
说明:这里可使用近似公式估算b的值:
当10*a>>b时,(10*a+b)^n-(10*a)^n≈n*(10*a)^(n-1)*b,即:
b≈41221398234/n/(10*a)^(n-1)=41221398234/5/180^4≈7.85,取b=7
以下各步都更加可以使用此近似公式估算b之值
差c=1508808527;与下一段合成,
c=c*10^5+下一段=1508808527*10^5+06000=150880852706000
第5步:a=187,找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:
(1870+b)^5-1870^5<=150880852706000,
b取最大值2,差c=28335908584368;与下一段合成,
c=c*10^5+下一段=2833590858436800000
第6步:a=1872,找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:
(18720+b)^5-18720^5<=2833590858436800000,
b取最大值4,差c=376399557145381376;与下一段合成,
c=c*10^5+下一段=37639955714538137600000

根号2等于多少 怎么计算的求过程

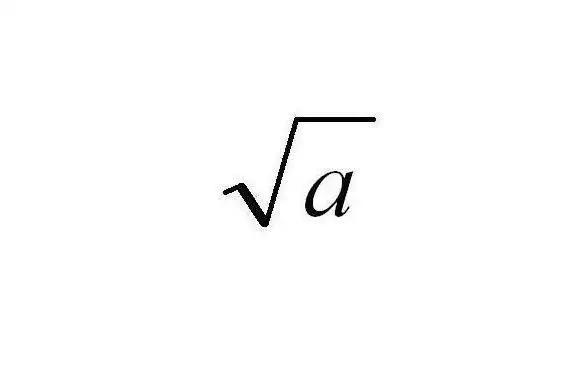
√2= 1.4142135623731 …… √2 是一个无理数，它不能表示成两个整数之比，是一个看上去毫无规律的无限不循环小数。早在古希腊时代，人们就发现了这种奇怪的数，这推翻了古希腊数学中的基本假设，直接导致了第一次数学危机。 根号二一定是介于1与2之间的数。 然后再计算1.5的平方大小……也就是一个用二分法求方程x^2=2近似解的过程。 扩展资料现代，我们都习以为常地使用根号(如 等)，并感到它来既简洁又方便。那么，根号是怎样产生和演变成这种样子的呢? 古时候，埃及人用记号"┌"表示平方根。印度人在开平方时，在被开方数的前面写上ka。阿拉伯人用 表示 。1840年前后，德国人用一个点"."来表示平方根，两点".."表示4次方根，三个点"..."表示立方根，比如，.3、..3、...3就分别表示3的平方根、4次方根、立方根。到十六世纪初，可能是书写快的缘故，小点上带了一条细长的尾巴，变成" √￣"。 1525年，路多尔夫在他的代数着作中，首先采用了根号，比如他写是2，是3，并用表示，但是这种写法未得到普遍的认可与采纳。 直到十七世纪，法国数学家笛卡尔(1596-1650年)第一个使用了现今用的根号"√"。在一本书中，笛卡尔写道:"如果想求n的平方根，就写作±√n，如果想求n的立方根，则写作³√n。"

怎么求根号2等于多少?

√2= 1.4142135623731 …… √2 是一个无理数，它不能表示成两个整数之比，是一个看上去毫无规律的无限不循环小数。早在古希腊时代，人们就发现了这种奇怪的数，这推翻了古希腊数学中的基本假设，直接导致了第一次数学危机。 根号二一定是介于1与2之间的数。 然后再计算1.5的平方大小……也就是一个用二分法求方程x^2=2近似解的过程。 扩展资料常用平方根： √0 = 0（表示根号0等于0，下同） √1 = 1 √2 = 1.4142135623731 √3 = 1.73205080756888 √4 = 2 √5 = 2.23606797749979 √6 = 2.44948974278318 √7 = 2.64575131106459 √8 = 2.82842712474619

根号（负4）的平方的算术平方根是多少

是4
根号（负4）的平方算术平方根是4

根号二的平方根是多少

+-1.189

（-2）²的平方根是多少？

解:±2
（-2）²=4,那么
根据平方根定义：一个正数如果有平方根，那么必定有两个，它们互为相反数。
上述题中4为正数，故平方根有两个，分别为：±√4 即±2

2的平方根是根号2吗？ 根号2的平方根是2吗？

2的平方根不是根号2，应该是2的平方根有2个，是±√2；
根号2的平方根也是有2个，是正负的4次根号2。
对于平方根来说，任何一个正数a的平方根有两个，它们互为相反数，记作±√a
其中 √a叫做a的算术平方根，0的平方根是0，负数没有平方根。

(-2.3）²的平方根是多少啊？

(-2.3）²的平方根是多少啊？
±2.3

－2是什么的平方根

(-2)²=4
所以-2是4的平方根

-2的平方的平方根是多少？9的平方根的立方根是多少？

您好：

√（-2）²=√4=2

³√（√9）=³√3



如果本题有什么不明白可以追问，如果满意请点击“采纳为满意回答”
如果有其他问题请采纳本题后另发点击向我求助，答题不易，请谅解，谢谢。
祝学习进步！

3的平方根是几

根号2加根号3等于多少，进来看讲解

2的平方根 是几?用式子表示出来!

√2=1.414
~如果你认可我的回答,请及时点击【采纳为满意回答】按钮~
~手机提问的朋友在客户端右上角评价点【满意】即可.
~你的采纳是我前进的动力~~
O(∩_∩)O,互相帮助,祝共同进步!

2的平方根是什么？

1.414

2平方根是多少

根号2，约等于1.414

（-2）²的平方根是多少

解:±2
（-2）²=4,那么
根据平方根定义：一个正数如果有平方根，那么必定有两个，它们互为相反数。
上述题中4为正数，故平方根有两个，分别为：±√4 即±2

2的开方是多少

±根号2